Sorting Algorithms
In this article, you will learn what sorting algorithm is and different sorting algorithms.
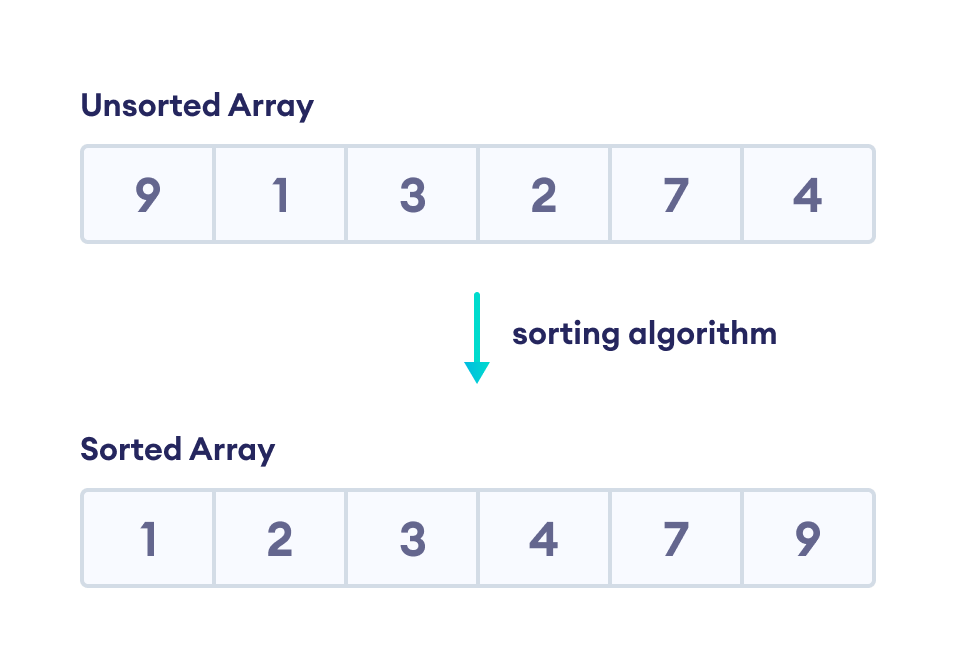
A sorting algorithm is used to arrange elements of an array/list in a specific order. For example,
Different Sorting Algorithms
Complexity analysis
| Sorting Algorithm | Time Complexity-Best | Time Complexity-Worst | Time Complexity-Average | Space Complexity |
|---|---|---|---|---|
| Selection Sort | n2 | n2 | n2 | 1 |
| Insertion Sort | n | n2 | n2 | 1 |
| Bubble Sort | n | n2 | n2 | 1 |
| Quick Sort | nlog n | n2 | nlog n | log n |
| Heap Sort | nlog n | nlog n | nlog n | 1 |
| Merge Sort | nlog n | nlog n | nlog n | n |
| Sorting Algorithm | Description |
|---|---|
| Selection Sort | Selection sort finds the smallest element in the array and place it on the first place on the list, then it finds the second smallest element in the array and place it on the second place. This process continues until all the elements are moved to their correct ordering. It carries running time O(n2) which is worst than insertion sort. |
| Insertion Sort | As the name suggests, insertion sort inserts each element of the array to its proper place. It is a very simple sort method which is used to arrange the deck of cards while playing bridge. |
| Bubble Sort | It is the simplest sort method which performs sorting by repeatedly moving the largest element to the highest index of the array. It comprises of comparing each element to its adjacent element and replace them accordingly. |
| Quick Sort | Quick sort is the most optimized sort algorithms which performs sorting in O(n log n) comparisons. Like Merge sort, quick sort also work by using divide and conquer approach. |
| Heap Sort | In the heap sort, Min heap or max heap is maintained from the array elements deending upon the choice and the elements are sorted by deleting the root element of the heap. |
| Merge Sort | Merge sort follows divide and conquer approach in which, the list is first divided into the sets of equal elements and then each half of the list is sorted by using merge sort. The sorted list is combined again to form an elementary sorted array. |